Teorie portfolia se zabývá optimální alokací aktiv na škále výnos-riziko (v angličtině se často používá termín mean-variance model).
Selektivní model Markowitze
Předpoklady modelu:
- investoři jsou racionální – tj. preferují větší výnos před menším a menší riziko před větším rizikem
- riziko je vyjádřeno směrodatnou odchylkou
- všichni investují na stejně dlouhé období (model je statický)
- známe směrodatné odchylky a korelace mezi aktivy (protože jsou konstantní)
- výnosy jsou sdruženě normální
Máme za úkol sestavit portfolio z n investičních instrumentů tak, že každému instrumentu přiřadíme určitou váhu w tak, aby součet těchto vah byl 1. Váhy mohou být i záporné (což znamená shortovat daný instrument), nebo můžeme krátké prodeje zakázat podmínkou $$w_i > 0$$.
Očekávaný výnos portfolia
Očekávaný výnos je daný jednoduchým vzorcem
$$ E(R_p) = \sum_{i=1}^n w_i R_i $$
tedy výnos portfolia je vážený průměr výnosů jednotlivých aktiv.
Riziko portfolia
Rozptyl výnosů portfolia bude dán výrazem
$$ \sigma_p^2 = \sum_i \sum_j w_i w_j \sigma_i \sigma_j \rho_{ij} $$
Směrodatnou odchylku spočteme jako odmocninu z této hodnoty. Pokud do portfolia zahrneme aktiva, která nejsou perfektně korelovaná, podaří se nám jejích kombinací získat výhodnější rizikově-výnosový profil než bychom získali koupí jakéhokoli jednotlivého aktiva.
Korelační koeficient ukazuje jen lineární závislost. Pro nelineární závislosti se používá Copula.
Efektivní hranice
Sestavujeme portfolio ze dvou aktiv, A a B, neuvažujeme krátké prodeje. Na grafu riziko-oč.výnosnost bude řešení všech možných kombinací, které lze sestavit z těchto dvou aktiv, záležet na jejich vzájemné korelaci výnosů:
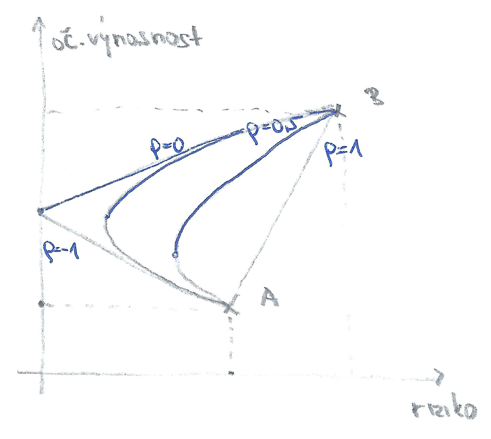
Bude-li korelace rovná 1, leží množina všech možných portfolií na přímce A-B. S klesající korelací má množina stále více prohnutější tvar. V případě perfektní záporné korelace je výsledkem lomená přímka dotýkající se svislé osy. Kombinace aktiv v tomto bodě bude mít za následek syntetizaci bezrizikového aktiva (z toho vyplývá, že bod, kde se tato přímka lomí, bude bezriziková výnosnost … a dále, že v případě perfektní záporné korelace by očekávaná výnosnost aktiva A byla nižší než bezriziková)
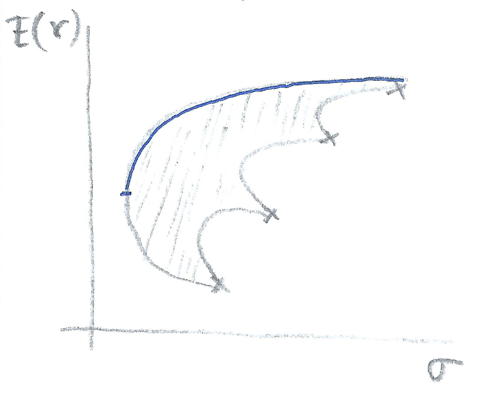
Máme-li více než dvě aktiva, je možností daleko víc. Následující obrázek ukazuje všechny možnosti vyšrafovaně. Racionální investor se bude snažit sestavit takové portfolio, které leží na modré čáře – tj. na nejzazší hranici všech možností s tím, že ho nezajímá ta dolní část pod bodem zvratu:
Situace bude ještě zajímavější, když tuto hranici efektivních portfolií složených z rizikových aktiv zkombinuji s aktivem bezrizikovým. Korelace mezi rizikovým a bezrizikovým aktivem je 0 – grafem všech možností pak bude úsečka tečující hranici efektivních portfolií:
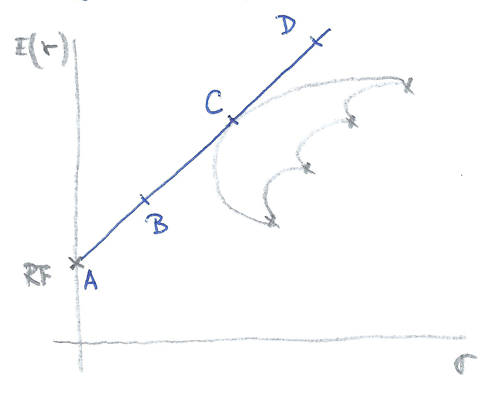
- A = všechny peníze investované do kvalitních státních dluhopisů
- B = mix bezrizikových a rizikových aktiv
- C = všechny peníze v rizikových aktived
- D = nákup rizikových aktiv na úvěr (s pákou)
Modrá přímka se označuje jako CML (Capital-Market-Line, přímka kapitálového trhu) a dala by se vyjádřit:
$$ E(R) = R_f + \frac{\sigma_p}{\sigma_m} ( E(R_m) – R_f ) $$
kde $R_f$ je bezriziková výnosnost, $\sigma_m$, $R_m$ je výnosnost efektivního rizikového portfolia (to, které leží na tečně) a $\sigma_p$ je riziko portfolia, které zvažujeme.
Jednoduchý indexní model
Problém je, že tento postup při větším počtu aktiv je poměrně výpočetně náročný (zejména korelační koeficienty, které rostou s druhou mocninou počtu aktiv). Proto se používá jednoduchý indexní model (Sharpe, 1963).
V něm není chování výnosové míry jednoho aktiva posuzováno se všemi ostatními, ale jen ve vztahu k tržnímu indexu. Matematicky můžeme psát:
$$ R_i = A_i + \beta_i R_m + e_i $$
- Ri – výnos z posuzované investice
- Ai – konstantní výnos z posuzované investice, který nezávisí na vývoji trhu
- beta – citlivost výnosové míry na výnosovu míru tržního indexu
- Rm – výnosová míra tržního indexu
- ei – náhodná chyba
Korelační koeficient mezi dvěma aktivy pak vyjádříme
$$ \rho_{ij} = \frac{\beta_i \beta_j \sigma_m^2}{\sigma_i \sigma_j}$$
Problémy
- Volatilita není konstantní, je stochastická a mění se v čase. Dost možná větším rizikem než samotná směrodatná odchylka je riziko její změny v budoucnosti.
- Korelační koeficienty nejsou konstantní, ale stochastické – mění se v čase a mnohdy velmi drasticky. I to je riziko, které není zahrnuto v tomto modelu.
- a spousta dalších.
Zdroje: